Let’s talk about carbon dioxide emissions from flying.

Friends, I have travelled in aeroplanes a good deal in my life, and I have benefitted a great deal from such travel, both personally and professionally. But now I am minded not to fly again until I take that fiery chariot to Valhalla.

My reasoning is that, with no need to travel professionally, I feel the pleasure I would gain from travel is not matched by the harm I would do – and the guilt I would feel – by emitting tonnes of carbon dioxide.

I personally know two other people who feel similarly. Curiously, these are both men of a similar age to me, who in the past have flown a lot, but who now feel they can no longer continue those habits. For both of them it is a significant sacrifice in their personal and professional lives.

However, most people I know don’t feel that way. In fact, they feel that flying is fantastic and they want to do as much of it as they possibly can! And while most of them are aware of the carbon dioxide issue, their judgement is that the pleasure they gain dramatically overwhelms any harm – and any guilt they might feel.

So Michael, tell me how you feel about this…

How do I feel? I wish that things were not so, but ultimately that is not the way the world is. And I feel it is important to genuinely respect the views of other people, even people with whom I disagree. By this I don’t just mean accepting what they say (while whispering under my breath “even though they’re wrong“). I mean genuinely respecting their views.  And indeed, I would not like to live in a world where everyone was like me!

Click on Image for a larger version. Graph from Our World in Data showing the growth of carbon dioxide emissions from aviation up until just prior to the pandemic.

Living any kind of modern life one inevitably emits carbon dioxide – typically a few tonnes per person per year. And I am no different. I still feel I “have to” drive a petrol car sometimes and I still occasionally eat meat – and even beef – sometimes. And global carbon dioxide emissions from flying are only one fortieth part of carbon dioxide emissions, and they bring immense happiness to travellers.

In short, we are all “carbon sinners”, and we each have our own calculus of balancing harms and benefits. And I would hope that other people would respect my calculus, and the quid pro quo is that I need to respect other people’s calculus too. And that is what I try to do.

And yet…

The carbon dioxide is still being emitted.

When someone describes “whizzing their family off to Thailand for Christmas” they are describing the emission of ~15 tonnes CO2. I feel that there really should be some way of discussing the issue without being rude. To me, this seems like an extraordinarily large amount of carbon dioxide, with each tonne making the world incrementally worse for our children.

But unless asked, I wouldn’t raise the issue. But it is an extraordinarily large amount of carbon dioxide to emit in a week!

Brave New World

This article is not about the technology of flying: I have written about that previously. Electrically-powered planes – which if powered from renewable electricity could be practically emissions free – may prove economical for short-haul flights up to (say) 200 kilometres (link). But the battery technology to create longer flights or carry larger payloads does not exist yet.

Similarly, Synthetic Aviation Fuel or Hydrogen-powered planes – in even the most optimistic scenarios – are decades away from significantly reducing carbon dioxide emissions.

So in my assessment there is no technological solution to this problem. For the foreseeable future, medium-haul and long-haul air flight will involve significant carbon dioxide emissions. And if – as I hope – we are nearing a peak in annual global emissions, then emissions from flying will become an ever more significant problem.

With due respect to everyone’s sensitivity, I really think we should be talking about this more.

Click on Image for a larger version. Graph from Our World in Data showing the growth of global carbon dioxide emissions. Could emissions be stabilising?

 

 

Arctic Sea Ice 2024

Friends, in the same way that one might check the back door before going to bed, I  regularly check in on Arctic Sea Ice just to relieve my anxiety that it might have disappeared while I wasn’t paying attention.

But it’s been a while since I took the trouble to download the data and make some graphs. Back in 2017, after The Guardian wrote a scare story about an imminent collapse in Arctic Sea Ice, I responded with a slight mis-quotation from Emperor Palpatine: “Everything is proceeding exactly as I had foreseen“. And after a mis-spent afternoon I can now report that this is still broadly true.

So for my benefit as much as yours, I present here an update to my 2017 graphs and a short commentary on how things are going.

Data

Every year the sea-ice floating on the Arctic Ocean and connected seas, freezes in winter, and then melts in summer, with the extent of the sea ice contracting and expanding by millions of square kilometres each year.

Scientists at the US National Snow and Ice Data Centre (NSIDC) process data from satellites in polar orbits to assess the extent and area of the sea ice. Extent and Area sound like synonyms, but in fact they are technical terms and NSIDC have a detailed explainer here. The distinction is subtle, but NSIDC generally use Sea Ice Extent, which is the area with more than 15% of sea ice.

The chart below shows monthly averages of the sea ice extent.

Click on image for a larger version. The blue line and black data points show the variation of the extent of Arctic Sea Ice (in millions of square kilometres) month-by-month since 1980. The green line shows the minimum extent in September each year and the red line shows the maximum extent in March each year.

Overall, one can sea that the sea ice extent is declining. But one of the curious features of the data is that the slope of the trend in sea ice maxima each March is less than the slope of the trend in sea ice minima each September. The figure below is a contraction of the top and bottom of the graph above to show this more clearly.

Click on image for a larger version. Contraction of the graph above to show more clearly the contrasting trends of sea ice maxima and minima. The blue line and black data points show the variation of the extent of Arctic Sea Ice month-by-month since 1980. The green line shows the minimum extent in September each year and the red line shows the maximum extent in March each year.

These trends indicate the ongoing change, but hide the complexity of many processes that have driven this change. Most importantly these graphs of sea ice extent do not reflect the thickness of the sea ice.

Detail in Depth

PIOMAS, the Pan-Arctic Ice Ocean Modeling and Assimilation System combines ice extent measurements with ice thickness measurements to produce estimates for Ice Volume – usually measured in the inconceivably large unit of thousands of cubic kilometres of ice.

Click on image for a larger version. PIOMASS data showing arctic sea ice volume. The blue line and black data points show the variation of the volume of Arctic Sea Ice month-by-month since 1980. The green line shows the minimum volume in September each year and the red line shows the maximum extent in April each year.

What’s the story?

I am not an expert in arctic climate, and it’s always dangerous to look for shorter term trends in long series of measurements. But using my Dunning-Kruger glasses, I think I perceive that the sea ice minima have broadly stabilised at their current levels since roughly 2010. This is visible in both the PIOMAS ice volume data and the NSIDC ice extent data. One possible explanation for this has to do with the way sea ice persists through the summer.

Click on image for a larger version. This graphic shows the previously-shown sea-ice extent and sea-ice volume data graphs with a red square highlighting the trends in sea ice maxima and minima since 2010.

Imagine putting a bowl of water in a freezer for a time T1 allowing ice to form. Then imagine removing the bowl from the freezer for a time T2 allowing the ice to begin to melt, and then repeating this process indefinitely. This is – very approximately – what happens in the Arctic.

Depending on the relative intensity of winter (T1) and summer (T2)  the ice may persist over the ‘summer’ or not. If it persists, then the new ice growth in the following winter will form around the previous year’s ice, and ice volume can grow from season to season. Eventually, there will be a balance with a persistent core of old ice, and layers of progressively younger ice.

The precise situation depends on the balance of winter cooling and summer heating, and the situation is stabilised by the very large amount of heat (so-called latent heat) it takes to melt and freeze ice.

• To heat 1 kg of water by 1 °C requires 4.2 kilojoules of energy.
• To melt 1 kg of ice at 0 °C requires 334 kilojoules of energy.
• To freeze 1 kg of water at 0 °C requires 334 kilojoules of energy.

The graphic below (From NSIDC: credit Tschudi et al., 2019b) shows the age of the oldest ice in a specific region coded by colour. The oldest ice – ice which persists over the summer – is coded as red. The two upper graphs show the areas with different ages of sea ice in March 1984 and March 2024. It is clear that the multi-year ice has almost disappeared.

The lower panel of the graphic below shows the relative fractions of ice of different ages. It shows that multi-year ice forms a declining fraction of sea ice, and that ice which is less than 1-year old forms ~70% (up from 40%) of the maximum sea ice extent.

Click on image for a larger version. Graphic from NSIDC showing the decline in ice which is many years old. The same colour scheme is used both upper and lower graphics with red representing multi-year ice and blue representing one-year-old ice.

The story that describes this data is – as I understand it – as follows. Warmer waters are entering the Arctic Ocean and melting the sea ice from below. Milder summers, are melting sea ice from above.

If the warming – from both atmospheric and ocean influences – continues, then eventually the stabilising effect of the large latent heat of ice will be overcome, and the sea ice on the Arctic Ocean will fully melt in summer. The North Pole will become the north pool.  At this point the Ocean will begin to warm significantly above 0 °C, slowing the re-growth of ice in the subsequent winter.

• Imagine that the final 334 kilojoules of (say, solar) energy is input to a kilogram of ice at 0 °C, finally melting it.
• The next 334 kilojoules would be enough to warm that kilogram to 80 °C!
• So once the ice has gone, there is the possibility for significant warming of the ocean, inhibiting ice formation the following year.

This recent paper suggests that sometime between 2035 and 2067, the Arctic Ocean will be regularly ice-free in September. So as our favourite baddie emperor might have said: Everything is proceeding as I had foreseen, but a bit slower than I had thought previously.

My Room Temperature

Friends, we are nearing the end of the heating season, and I was just browsing through the data (taken every two minutes through the last year!) and I wondered how the temperature in the middle of my house had varied through this last winter. The answer is that the temperature through the winter has stayed at a remarkably stable 21.5 ± 0.4 °C. Allow me to show you the data.

The whole data set

Click on image for a larger version. Graph showing the variation of room temperature in my home over the last year. The graph shows more than a quarter of a million data points. Also plotted is the variation in external temperature shown as a thin line and also the daily average temperature shown as a thick blue line.

Notice that last summer the internal temperature rose as high as 25 °C when the external temperature rose to 30 °C during the day. But in winter, the temperature stayed relatively stable even when the external temperature fell below 0 °C.

Aside from the temperature we can also plot the heat delivered by the heat pump.

Click on image for a larger version. Graph showing hourly averages of the heating power delivered by the heat pump.

In summer the heat pump is used for delivering hot water, but in winter the heat pump also delivers heat for space heating at a rate of roughly 1.5 kW (i.e. 36 kWh/day), with a peak heating of 3.6 kW in January’s cold spell. Let’s place the previous two graphs together.

Click on image for a larger version. The upper part of the graph shows the variation of room temperature and external temperature in degrees Celsius and the lower part of the graph shows heating power in kilowatts.

Putting these two graphs together we can see clearly the correlation between heating power and heating demand – the difference between internal and external temperatures. We can see that on the coldest day the maximum hourly average of the heating power was ~3.6 kW when the heating demand was approximately 23 °C ± 2 °C. This gives us an estimate for the heat transfer coefficient of the house as 3,590 W / 23 °C = 156 ± 12 W/°C.

Winter

Click on image for a larger version. Data from the winter of 2023/24. The upper part of the graph shows the variation of room temperature and external temperature in degrees Celsius and the lower part of the graph shows heating power in kilowatts. Also shown are the averages of the data over the period shown.

Looking more closely at the winter data four things occur to me.

• The data are not bad. Most of the time the internal temperature was in the range 20.5 ± 0.4 °C – and the house was comfortable all winter.
• However, the actual set temperature was 20 °C. And in the coldest weather the internal temperature fell to between 19 °C and 20 °C. The heat pump has more than 5 kW of available power at 0 °C, so I am not sure why it didn’t compensate to keep the internal temperature stable. This is a failure of the control system and I will be twiddling some settings carrying out investigations to try and improve this for next winter.
• The average heating power over winter was roughly 1.6 kW which is just 32% of the nominal heating power of the pump. Sadly, like most heat pumps, the Vaillant Arotherm 5 kW can only smoothly alter its output down to 40% of its nominal capacity. In other words, most of the winter it has to switch on and off – typically once an hour – in order to deliver heat at the required rate.
• Finally, the average heating power over winter was roughly 1.6 kW or 38.4 kWh/day. At an average COP of 3.5 this corresponds to about 11 kWh of electricity per day. We filled the battery (capacity is just over 12 kWh) with electricity at 7.5 p/kWh during the night, and then ran using the battery until it ran out. We then had to buy some full price electricity at the end of each day. But during December and January heating costs were still just ~£3.50/day.

Click on image for a larger version. Monthly costs for electricity over the last year. The cost for April 2024 is an estimate.

 

Is a 100% Renewable Energy Grid Possible?

Friends, regular readers will be aware that I am very much in favour of electricity generation from renewable sources – primarily wind and solar. And the reason I am in favour of these sources of electricity is that they have very low associated emissions of carbon dioxide. So switching rapidly to these sources might allow us to continue to enjoy relatively cheap access to energy while reducing the possibility of catastrophic climate change.

At the turn of the century it was thought that the fraction of renewable resources that could be incorporated onto the grid was rather small: between 5% and 10%. But that has not proved to be the case: last year the UK generated 37.2% of its electricity from renewable sources – more than it generated using fossil fuels (33.4%) (Link). This fraction will likely increase for the next couple of decades. But can it reach 100%?

I have been sceptical about this but considered that a grid with some high fraction of renewables (80% to 90%) would be not bad – and getting to this point would take a couple of decades, and that by that time we might have figured out how to close the gap to 100%.

Recently, I have become less sceptical and I now consider that a 100% renewable grid is possible. And so I thought I would write down my reasoning…

Models with less than 100% Renewable Electricity.

First there are simple models that take the existing hourly patterns of generation from wind and solar, and scale it by different factors.

For example MyGridGB has been running such a model for several years now, modelling how a hypothetical 2030 grid would meet current demand hour-by-hour. This is not a 100% renewable grid – but being near term it is a much more practical possibility. The assumptions are that:

• Hinkley C nuclear power station will come on line
• Nominal Wind capacity will be about 50 GW compared with 30 GW in 2023
• Nominal Solar generation will be around 40 GW compared with 16 GW in 2023
• Some biomass and gas but no coal.
• 100 GWh of electricity storage (Approx. 6x more capacity than Dinorwig and Cruchan hydro storage). UK grid battery storage is currently about 4.6 GWh.

These are sizeable upgrades but quite achievable and broadly in line with what is in “the project pipeline”.

And the impact? Broadly this change would lower the annual carbon intensity of UK electricity to ~100 gCO2/kWh from its current ~200 gCO2/kWh. For example, the figure below shows how demand was met from 11th March 2024 to 7th April 2024 and how that same demand would be met with an improved grid.

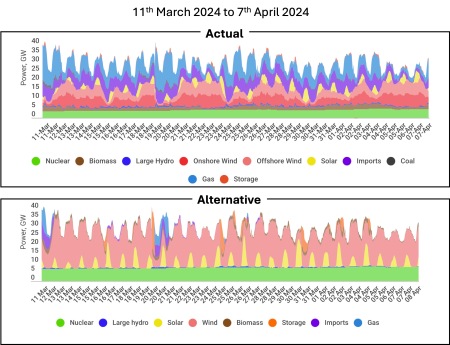
C

The demand is exactly the same in both graphs, but notice the absence of blue (gas generation) from the lower graph. In this hypothetical low-carbon grid, gas generation would only be used rarely even in the relatively cold month of March.

Similar studies have been carried out for New Zealand, California and Australia, and for each country a different mix of solar, wind and storage is optimal. So for the UK we would choose a wind-weighted mix as opposed to California which would have a higher weighting of solar. These studies are helpful in showing the rough scale of endeavour required, and establishing the optimal mix of generating resources. But they are unrealistic for several reasons.

• Demand: They do not consider how electricity demand might change in the future. This requires estimating the increased demand as heating and transport become increasingly electrified. However, neither do these studies consider the effect of demand modification by variable pricing, which will generally reduce peaks in demand.
• Stability: They do not consider the stability of the grid as an electrical system. I’ll talk more about this below.
• Extreme Variability: And they do not consider the most extreme possible cases of variable renewable generation – weeks on end of low wind and solar generation.

So these models are useful for establishing the basic feasibility of grids with high renewable fraction. These models all feature some storage – but typically just a few hours of demand – not weeks-on-end of storage. And the amount of wind and solar generation is scaled not so that maximum generation meets demand, but so that minimum generation meets demand. This means that when renewable supply exceeds demand, the renewable energy must be used for something else, or curtailed i.e. just switched off. It is not yet clear what that ‘something else should be. Obvious candidates included charging batteries or some other form of storage – perhaps generating hydrogen for later use. But the economics of this kind of process are not yet clear.

Addressing Weaknesses

I have recently finished reading a lengthy review :”On the History and Future of 100% Renewable Energy Systems Research” which addresses some of the weaknesses of the simple models I have described above. This paper explicitly considers grids that are  100% renewable: i.e. no gas or coal.

 

Notable amongst the authors are Mark Z Jacobson and Auke Hoekstra. Jacobson is the author of “No Miracles Needed: How todays technology can save our climate and clean our air.” and Hoekstra has authored in-depth analyses showing the positive effects of electrification of transport – including the inevitability of the electric freight trucking.

The authors identify five criticisms concerning the feasibility of 100% renewable grids, and address each criticism directly.

1. Energy Return on Investment.
2. Variability and Grid Stability.
3. Cost versus Conventional Grids.
4. Raw Material Demand.
5. Community Disruption and Injustice.

Criticism#1: Energy Return on Investment (EROI)

It has been asserted historically that the idea of a 100% renewable grid does not make sense because the energy required to construct the generation (PV and Wind) is less than the energy generated by the technology over its lifetime. Whatever justification this might have had historically, this is not the case now. Reasonable estimates suggest that the over their generating lifetimes:

• Solar PV installations have an EROI between 15 and 60.
• Wind turbines have an EROI between 20 and 60.

In other words they generate ~ between 15 and 60 times as much energy as it cost to build them. So the energy to construct these renewable generating resources is just a few percent of the energy generated. Initially, these resources may require fossil fuels to enable their construction. But as industrial processes electrify, and as the renewable fraction of grid generation increases, less and less fossil fuels will be required to construct each subsequent generation of renewable resource.

Criticism#2: Generating Variability and Grid Stability

It is a simple fact that much larger fractions of renewable electricity can operate on the grid than was anticipated even a few years ago. But can it reach 100%? The authors of this paper argue that yes it can, but the ‘new grid’ needs to operate with a new paradigm.

Historically generation consisted of ‘baseload’ generators that operated more-or less continuously, and so-called ‘dispatch-able’ resources that could be switched on at few moments notice from a grid control centre. To meet the new realities of a renewable grid, this  “baseload plus dispatch-able generation model” needs to be revised.

The ‘New Grid” will probably not have a separate “baseload” category, and will incorporate more diverse sources of generation, international interconnections, storage, and demand response. So this new grid will certainly be more complex to manage, but the authors argue that given modern computing resources and engineering understanding, it is perfectly manageable.

To understand why the authors adopt this position, it is important to understand that although renewable resources are variable, they are predictable around two days in advance with reasonable confidence. As we approach a 100% renewable grid, use of gas generation will grow rarer and rarer. Initially the 100% renewable grid will only be achievable for at first days at a time, then weeks, then seasons, and finally whole years.

This progression will be the result of increasing solar and wind generation and increasing storage and the techniques for managing the generating will likely develop over a decade or so as the grid approaches 100% renewable electricity. But throughout this transition some gas generation is likely to be retained as back up for intermittent use. In terms of emissions, switching on gas-fired generation for 10 days a year will make very little difference.

The basic tools that will help the ‘New Grid’ to cope will be:

• Nominal oversizing of the wind and solar resources.
• Larger interconnections with geographically remote sources.
• Demand response
• Increased Storage
• Sector coupling i.e. using excess generation capacity for some useful purpose such as electrolysis of water to produce hydrogen.

The issue of grid stability is difficult to explain, but allow me to try. The grid consists of alternating current (AC) sources of electricity in which electric current flows back and forth along wires 50 times per second. It is critical that all the sources on the grid operate in phase i.e. that every power source – no matter where it is in the country –  ‘pushes’ electric current in synchronisation otherwise the power from each source will not add up.

Currently (no pun intended) this synchronisation is achieved because the rotating turbines in thermal power stations weigh hundreds of tons and rotate at high speed providing inertia to the grid.

• If more energy is drawn from the grid than is being supplied, the frequency of the grid falls fractionally and more sources are brought on line.
• Similarly, if more energy is being supplied than consumed, then the frequency of the grid rises, and generating sources are taken off-line.

Keeping the grid frequency stable and synchronising generation is critical to the safe and efficient operation of the grid. At the moment, the rotational inertia of generating technology additionally performs a stabilising role. But in a grid with 100% or near to 100% renewable sources, the inertia that keeps the grid stable needs to be deliberately added. This can achieved by rotating stabilisers or by so-called grid-forming inverters. This represents a change to the way the grid operates – but the challenge is neither insuperable nor particularly expensive.

Criticism#3 Cost

The cost of any large project is difficult to anticipate. But the authors point out that historical estimates of the the cost of renewable energy projects are significant overestimates because of the the effect of the learning curve. This is discussed extensively in this 2020 article by Max Roser on Our World in Data. And the cost reductions in renewable technologies have been staggering, and contrast dramatically with the cost increases in competing spheres, such as nuclear generation.

The three graphs below show the price reductions in batteries, solar PV cells, and all generation technologies. In the face of this, the authors argue that realistic incorporation of the effects of the learning curve result in cost estimates that are cheaper or at least competitive with conventional generation. And of course, the cost of business-as-usual in terms of damage to our climate is not considered. Taking account of this, a renewable grid is a no-brainer.

Click on image for a larger version. Graphic from Our World in Data showing the reduction in the price of Lithium Ion Batteries versus year. I have extended the trend to illustrate what is yet to come. Price cuts are still ongoing.

Click on image for a larger version. Graphic from Our World in Data showing the reduction in the price of solar PV modules which are combined into solar panels cumulative installed capacity. Price cuts are still ongoing.

Click on image for a larger version. Graphic from Our World in Data showing the change in the price of the Levelled Cost of Energy (LCOE) for a variety of generation technologies versus their installed base. Notice that renewable technologies tend to get cheaper as their installed base increases.

Criticism#4: Raw Materials Demand

Criticisms of a renewable energy grid often highlight the raw materials needed to construct the batteries, solar panels and wind turbines. While there will no doubt be issues as we scale up to a renewable energy world, the amounts of materials involved are small compared with current demands, and are dwarfed by the amount of oil and coal currently mined. Of course, oil and coal are high polluting and can only be used once: the metals mined for renewable technologies can all be recycled. For scale, the graphic below shows the scale of mining in 2022.

Click on image for a larger version. Graphic from The Visual Capitalist illustrating the relative mass of metals mined in 2022.

Attention is often drawn to the use of particular minerals, particularly cobalt (used in the first generation of lithium-ion batteries used for TVs) and so-called rare-earth metals Neodymium and Dysprosium used in the magnets incorporated into some motors and generators. Personally, I think these are non-issues.

The use of cobalt as a catalyst in oil-refining was never an issue until cobalt began to be used in EV batteries. Happily, modern lithium iron phosphate batteries do not use cobalt, but sadly, cobalt is still being used to manufacture the fuel for internal combustion engine vehicles. Similarly, the latest motors from Tesla avoid the use of any rare-earth magnets.

Criticism#5: Community Disruptions and Injustice

Friends, community disruption and injustice are sadly features of our modern world. And they have been for centuries. And these issues are real and serious. But that people wanting to extend the life of fossil fuel extraction – the cause of catastrophic climate disaster – should address such criticism against renewable energy projects is – frankly – laughable.

Summary

So can we build a grid with 100% renewable sources? In short, yes, I do think it’s possible.

The ‘New Grid’ will not be identical to the ‘Old Grid’. And it will have weaknesses, particularly in its early decades. Most notably, until interconnections extend between continents, it will be vulnerable to – for example – volcanic events such as occurred in 1816:  ‘The Year without a Summer‘. However, it will be less vulnerable than our current grid to hostile geopolitical situations which restrict the availability of key fuels. It is an arguable which of these possibilities might be considered more likely.

But the overwhelming advantage of a 100% renewable energy grid is that directly addresses our climate crisis. Is there an alternative? The only plausible alternative is a grid based on nuclear power, but given our collective inability to safely dispose of the nuclear waste we have created over the last 50 years, and the extremely high cost of nuclear generation, I simply cannot see this happening. In contrast, progress towards a future based on renewable energy is proceeding at an ever accelerating pace.

Dust and Water

Dust by Jay Owens and The Three Ages of Water by Peter Gleick.

Friends, I have recently read two books that have caused me to re-evaluate – in the words of Peter Gleick – the true value of water. The first book, Dust, considers the role of dust in human culture. And the second, The Three Ages of Water, describes the critical importance of fresh water for all life on Earth. Partly to help me recall the contents, I thought I would write a précis of the two books, and I hopefully you will find this of interest too.

Dust

Dust may seem an odd topic for a book, but it in fact dust is an intrinsic part of the natural world and plays an outsize role in many geophysical processes. As materials break down, they turn into small and smaller particles and at some point – below around about a tenth of a millimetre or so – we somehow lose consciousness of them as individual particles. But the materials are still there. Crucially, when not bound by water, particles of this size are small enough to be lifted by the wind and held aloft.

Jay Owens begins her assessment of the significance of dust in her own flat as she reflects on the astonishing amount of otherwise invisible dust made visible in the beams of sunlight. This is the start of a world-wide journey.

She first revisits the origin of the concept of ‘dusting’ – a task which arose from combination of the appalling particulate pollution from coal burning, and the development of consumer goods which needed to be displayed. She argues that the idea of household cleaning as “women’s work” led to the oppression of women throughout the 19th and 20th Centuries.

She visits Owen’s Valley, California where in the 1920’s entrepreneurs from Los Angeles acquired – through techniques of dubious legality – water rights that underpinned the growth of Los Angeles and led to the destruction of Owen’s lake, which became a source of toxic dust, and led to the desolation of a fertile valley. And she visits the land at the heart of the creation of the dustbowl in the US in the 1930’s.

Likewise she visits the Aral Sea where in the 1960’s soviet planners re-directed the sources that fed the Aral Sea in order to grow cotton. Since then the sea has all but disappeared, leading to toxic dust storms that have led to the desertification of a once fertile ecosystem.

Click on image for a larger version. USGS Landsat images of the Aral Sea in 1992 and 2020. Even in 1990 the sea, once the 4th largest freshwater lake on Earth, had already undergone significant contraction.

She visits the areas around atomic bomb test sites and investigates the lasting impact of the clouds of invisible radioactive dust that spread across the USA from the explosions.

Click on Image for a larger version. From the Downwinders Website, this graph shows the dose of radioactive Iodine -131 at locations across the US as a result of dust particles from atomic bomb tests.

And she visits Greenland to see the effect of particles of black carbon on the melting of the ice sheet.

Click on Image for a larger version. The upper image from the American Museum of Natural History shows a section of an ice core from the Greenland Ice sheet. The yearly bands are clearly visible. The lower graph shows analysis of such ice cores revealing the amount of black carbon dust deposited year by year over the last 800 years.

Throughout all her travels, Jay Owens emphasises the outsize role that tiny particles of dust play, and notes that somehow it always the less powerful groups in society that suffer. Although her writing is polemical at times, I feel that the book has nonetheless raised my consciousness of dust. Previously I had thought of dust as being incidental or peripheral, but in fact, if you look for it, dust is everywhere.

Water 

We all know that water is important, but Peter Gleick’s aim in writing this book is to urge is to see the true value of water.

In the first age of water, he discusses the role of water in the prehistory of the solar system, our planet, and the development of life, and leads us eventually to the critical role of water in the first civilisations that we know of, circa 5,000 BC.

What I had not fully appreciated is the profound extent to which control of water – via the construction of dams and irrigation structures – was at the base of all of the activities of these civilisations. And that loss of control – either via floods or drought or conflict – led to the collapse of societies, over and over again.

The second age of water – the age in which we are now living – is the age in which we ‘mastered’ fresh water. We can now control the flow of water from mountains to the sea, and we can ‘mine’ water from deep underground. And we know how to create potable water almost anywhere on Earth. And yet after perhaps 150 years of mastery, we find ourselves in a very difficult place.

Most critically, despite the UN declaring water to be a fundamental human right – with a nominal target of 50 litres per day – millions of people on Earth still lack basic facilities for drinking and hygiene.

Click on Image for a larger version. Based on weekly meter readings, the graph shows the household usage of water for myself and my wife is on average around 100 litres per person per day.

Additionally, and I don’t need to tell this to UK readers, many of our rivers and water courses are polluted to the point where ecosystems have been damaged.

Perhaps the defining feature of the second age of water is that we have treated water as being “ours” and considered any water which is not captured or used to be wasted or ‘lost’.

And worldwide we have mined “fossil” water collected in aquifers over thousands of years to create agricultural systems that have flourished for a few decades, but which are – literally – unsustainable. If we run out of almost any other substance, we can find a substitute, but there is no substitute for water.

The third age of water is the age which Gleick believes we are entering, and age in which we truly value water as the unique element around which all ecosystems are constructed. Some features of this age are:

• Reduction of the amount of water that we use, domestically, industrially and agriculturally – but with no reduction in the utility we extract from the water.
• Valuing potable water for the wonderful product that it is and using ‘grey’ water for many of the functions for which we currently use potable water.
• Valuing the ecosystems within which all life exists, even to the point of giving rivers and ecosystems legal representation. Already, the US is removing dams to allow the slow re-building of natural water courses, and wetland restoration projects are underway world -wide.

I found the book by turns educational and inspiring. Although hearing of the phenomenal degradation left over from the second age of water, I feel that we have now universally accepted that it’s generally a bad thing when rivers catch fire. [Note added: Randy Newman wrote a song about one of the better known river fires]

As I was reading the book reports were unfolding of the appalling behaviour of Thames Water, the company that supplies my own water. And I was reminded that water is still of fundamental importance and that as in the civilisations of Early Mesopotamia, kingdoms could fail if water was not well-managed.

Water & Dust 

As regular readers will know, I am personally immersed in issues around our Climate Crisis. And I try to avoid becoming too involved in our other ongoing ecological crises – things can get very depressing! But together these books have raised my consciousness without getting me down too much. The Three Ages of Water in particular sets out a very positive and achievable agenda for change.

Saving the World One Day at a Time

Friends, please accept my apologies, this post is another song. It’s on YouTube at this link. I think this thing with songs is probably just a ‘phase’ and I’ll get back to calculating something soon.

The YouTube version is just me singing and accompanying myself with a guitar, but if you prefer an amateur ‘rock’ arrangement, there is a version on Soundcloud at this link.

Why?

Friends, I write songs and sing about the things which affect my life. And I am immersed in the Climate Crisis. And I don’t think I am alone. Even people who are not active in any way understand that “something is not right”. And singing is a way to communicate with the clientele of The Mason’s Arms, very few of whom follow my blog.

Lyrics

Friends, I’m just an old man, trying to live my life in peace.
I’m no kind of… revolutionary.
But there’s something going on. Something really wrong.
And it affects my kids and that means I can’t sleep…

So… I’m trying to save the world, one day at a time,
Making up for what my generation’s done.
I’m trying to save the world, one day at a time,
Because my children have to live here when I’m gone.

The Good Earth gives us everything we need.
But the Earth’s in pain, she’s begun to scream and bleed…
The Good Earth doesn’t need us. Doesn’t need to feed us.
So when the Earth’s in pain – we’d best take heed.

So… I’m trying to save the world, one day at a time,
Making up for what my generation’s done.
I’m trying to save the world, one day at a time,
Because my children have to live here when I’m gone.

We’ve been burning oil and coal, for about two centuries.
And now the whole world’s getting hotter every year.
Some say we can’t afford to stop. But I say we can’t afford to not!
Because no amount of money, can repair Earth’s atmosphere.

So… I’m trying to save the world, one day at a time,
Making up for what my generation’s done.
I’m trying to save the world, one day at a time,
Because my children have to live here when I’m gone.

I am just one person, you’re one person too.
And these problems seem impossibly too grand.
But we all care for our kids. And if each of just did,
What we need to, then our kids might have a chance.

So… Let’s try to save the world together, one day at a time,
Let’s make up for what our generation’s done.
Let’s try to save the world together, one day at a time,
Because our children have to live here when we’re gone.

So… Let’s try to save the world together, one day at a time,
Let’s make up for what our generation’s done.
Let’s try to save the world together, one day at a time,
And hope our children will forgive us when we’re gone.

©Michael de Podesta 2024

Can I believe my Vaillant Heat Pump COP?

“A person with a watch knows the time,
but a person with two watches is never sure“

Friends, I love measuring things. Being able to use a thermometer or a voltmeter or pH [not Ph!] meter to measure an apparently inaccessible quantity is like having a superpower. It enables one to perceive an otherwise invisible world.

But if one measures the same quantity with two different measuring instruments, they will – in general – disagree. And if that disagreement is significant, one’s initial insights from the measurement become clouded with doubt. And eventually one has to decide which one of the instruments is reporting closer to the true answer. This is both an everyday occurrence in metrology labs (and my house) and also a profound philosophical question about measurement.

This article describes how I am resolving my philosophical confusion with regard to measurements my 5 kW Vaillant Arotherm Plus heat pump. The installation reports its own estimate for the electricity it consumes and the heat it delivers to my house. But I also monitor the electricity consumed and heat delivered using separate measuring instruments installed as part of a Metering and Monitoring Service Package (MMSP).

In this article I will compare the readings from the Vaillant and the MMSP system and show that although qualitatively similar, they disagree significantly, and the Vaillant system displays many signs of being not very reliable. But it appears to have changed its behaviour in late 2023 and may be improving.

Data

The MMSP system monitors an electrical meter and a heat meter every 2 minutes and logs the data on line. I read these meters as part of my Saturday meter-reading ritual – and I log the readings which were effective at midnight on the Friday night/Saturday morning.

The Vaillant system stores its estimates for electricity consumed and heat delivered on line and I can access them as daily, weekly, monthly or annual summaries using the myVaillant app on my iPhone. I stepped back week-by-week to the start of my installation and recorded the Vaillant estimates by hand into a spreadsheet.

[Note added moments after publication: In fact, if I were not a complete idiot, I might have noticed that there is a button to download a whole year of data at time. Doh!]

Click on image for a larger version. Screenshots from the myVaillant iPhone app for three different weeks from December 2021 to March 2024. The three full screen images show weekly summaries of data for electricity consumed, environmental yield, total heat generated and the amount of domestic hot water generated. Further details are available from each measurand as shown in the two screenshots at the left. Notice that in all but one of the screenshots, every number ends in “.0”.

Because I typed in the Vaillant data by hand, it was immediately obvious to me that there was something very fishy about the data. For prolonged periods, the quantities recorded both per day and per week (kWh readings for electricity consumed, environmental yield and domestic hot water) were all exact integers i.e. the data read “XX.0” rather than “XX.1” or “XX.2” etc. Of the 134 weekly readings I recorded, 51% of the electricity readings and 36% of the heat readings ended “.0” when one would expect typically about 10%.

Nonetheless when plotted against the MMSP readings the Vaillant data appeared qualitatively similar. One would not expect the Vaillant data to be exactly the same as the MMSP data because the Vaillant data run from Sunday to Saturday night – a one day shift compared with the MMSP data.

Electricity Data

Click on image for a larger version. Electricity consumption used to run the heat pump (kWh/day averaged weekly) estimated by the MMSP installation and the Vaillant heat pump. 10 kWh/day corresponds to around 420 W of continuous power.

Looking at the electricity consumption data it’s not easy to spot a consistent difference between the two systems. But if one records the cumulative consumption, then the different weekly periods become irrelevant. When one does this it becomes apparent that the Vaillant data are consistently lower than the MMSP data by about 7.4%.

Click on image for a larger version. Cumulative electricity consumption used to run the heat pump (kWh) since installation estimated by the MMSP installation and the Vaillant heat pump. The Vaillant system underestimates total consumption by 7.4%.

This 7.4% error amounts to approximately 500 kWh over 134 weeks or 3.7 kWh/week or 0.23 kWh/day or an error of 22 watts of continuous power. This both (a) not very much but also (b) much greater than I can explain. My first suspicion was that the Vaillant may not be measuring the power used for the auxiliary hydraulic pump used to circulate water around my radiators. But looking at the difference data in detail, I see no evidence that there was change in October 2023 when I removed the hydraulic pump.

Heat Data

Click on image for a larger version. Heat delivered to my home by the heat pump (kWh/day averaged weekly) estimated by the MMSP installation and the Vaillant heat pump. 50 kWh/day corresponds to around 2 kW of heating power.

Looking at the heat delivered data one can see that the MMSP data for winter – when most heat is delivered – seem to be consistently higher than the equivalent Vaillant data.  It seems as though this difference is less this winter of 2023/24. If one records the cumulative consumption, then it becomes apparent that the Vaillant data are consistently lower than the MMSP data by about 16.4%.

Click on image for a larger version. Cumulative heat delivered by the heat pump (kWh) since installation estimated by the MMSP installation and the Vaillant heat pump. The Vaillant system underestimates total heat delivered by 16.4%.

Seasonal Coefficient of Performance (SCOP)

Click on image for a larger version. Seasonal (52 week average) COP estimated from 12 months after installation  and running continuously until March 2024 estimated by the MMSP installation and the Vaillant heat pump. The Vaillant system underestimates SCOP – but the amount of underestimation appears to be getting less since reducing the flow rate in November 2023.

Having compiled the weekly data, I calculated the Seasonal Coefficient Of Performance (SCOP) by finding the ratio of total heat delivered to the total electricity consumed over the preceding 52 weeks. I then calculated this as a running quantity versus time.

Considering first the MMSP data. The first SCOP calculation is about 3.53 covering the 12 month period from August 2021 to July 2022, and plotted on August 2022. As the winter of 2022/23 proceeds the SCOP falls to about 3.45 – probably because the winter of 2022/23 was colder than the preceding winter of 2021/22. And the SCOP is currently (March 2024) at a similar level. I have changed some operational settings during this period (details later) but my conclusion from the MMSP data is that heat pump is operating in a roughly similar manner to when it was installed in August 2021.

Moving on to the Vaillant data, we see a more complicated story. First of all, based on the anomalous “.0” values, which are especially prevalent in the early data, I conclude that the initial data is just wrong: it gives a SCOP of about 3.06 when the MMSP value was 3.53. This is a large error – and when I looked at this previously…

• Initial Heat Pump Review – after 1 year but before the myVaillant App
• myVaillant App Review

… I basically dismissed the Vaillant data as being ‘indicative’ at best.

However, looking at the graph above it’s clear that something happened in November 2023. As more recent data replaced older data, the Vaillant estimate for SCOP has risen consistently and is currently 3.32 compared with 3.43, the MMSP estimate. With this level of discrepancy, the Vaillant data are now good enough to be more than indicative: even borderline useful.

What happened in November 2023?

A couple of things changed in the Autumn of 2023. In October 2023, everyone’s favourite urban plumber Szymon Czaban removed the low-loss header from the system, and a few weeks later I reduced the flow rate through the system to 50% of it’s maximum value. One can see a small step-increase in SCOP in the MMSP data when I reduced the flow rate I think one or both of these changes might possibly be behind the change in quality of the Vaillant data.

With the low loss-header in place, the heat pump could circulate water rapidly – approaching 1,000 litres per hour – and there would be a very low difference in temperature between the ‘flow’ and ‘return’ temperature of the water circulated by the pump – typically just 1 °C or less. So if the heat meter – which measures the difference between the flow and return temperatures – had a small mis-calibration, then reducing the flow and consequently increasing the temperature difference -might well improve its accuracy.

However this is all just speculation. But the Vaillant results do seem to be changing.

Summary: Can I trust my Vaillant SCOP? And can you?

Comparing the MMSP and Vaillant data, I find that – reaching beyond my philosophical confusion – I just don’t believe the initial Vaillant data. The issue where every quantity measured every day ends in an exact number of kWh is deeply suspicious. It’s like finding someone with jam around their mouth swearing that they didn’t eat the doughnut. So I trust the MMSP readings over the Vaillant readings – and if the trend in the Vaillant data of improved agreement with the MMSP data continues, it may eventually prove useful.

But based on what I have seen on my installation, the Vaillant cannot be trusted to accurately report COP and SCOP. I wish it weren’t that way, but that’s what I see. However, I can’t speak for what you can trust in your installation. Of course I could sign up for open energy monitor (see Heat Pump Monitor for installed systems) and have a third system monitoring my installation. Mmmmm.

Reanalysis

Friends, this article is about one of the most breathtakingly bold undertakings in climate science, an endeavour modestly called: reanalysis. The article is a little bit technical, and there are tragically no songs or videos like the last two articles, but there will be fascinating pictures such as the ones below.

Click on image for a larger version. Image from the Copernicus ‘pulse’ web site showing how global average sea-surface temperature anomaly has changed through the months of the year. Last year (2023) and this year (2024) are much warmer than any year since 1979. Notice that the data is updated daily.

Click on image for a larger version. Image from the Copernicus ‘pulse’ web site showing the global sea-surface temperature anomaly on 1st March 2024.

If we consider the map above, the detail is fascinating, but after a moment or two you might wonder something like:

“How do they know what the temperature is everywhere on the Ocean surface? Surely they don’t have that many thermometers?

The maps and temperature anomalies shown above are known technically as Reanalysis Products, and they are not quite direct measurements, but neither are they pure calculations. Allow me to explain.

Weather Forecasting

Click on image for a larger version. Image from the Wikipedia article on Numerical Weather Prediction showing qualitatively the elemental volumes used in models of Earths atmosphere.

How does one begin the process of starting a weather forecast? One starts with information about the state of the atmosphere at a particular time. This information is determined from a variety of sources: standard meteorological stations on the ground; buoys at sea; weather balloons (which are launched simultaneously around the world); and most significantly from satellite information about the temperature and humidity at various heights in the atmosphere.

With this information one can prime a computer model of the atmosphere. The model divides the atmosphere into a number of volume elements, and based on all the data, estimates, the temperature, pressure and humidity within each volume element. The model then uses the laws of physics to calculate how – over time – heat and moisture will be transferred between volume elements: this is the process of “running” a weather forecast model (numerical weather prediction).

But before running the forecast model, there is an additional step required. The data sources do not provide data for every volume element in the model. Or perhaps different data sources disagree about the temperature of some volume elements. So before running the forecast model, the temperature, pressure and humidity of the blank elements have to be estimated. This is done by interpolation between the known volume elements in a way which is consistent with the laws of physics. In this way the initial state of the atmosphere can be specified at every volume element – and this is the input to the forecast model.

Reanalysis

Normally this estimate of the initial state of the atmosphere would be discarded as soon as fresh data became available – leading to an updated forecast. But instead of discarding it, the estimate of the state of the atmosphere can be re-purposed, or re-analysed.

There are three processes at the heart of ‘reanalysis’.

• Assimilating vast amounts of data
• ‘Filling in’ gaps between the data.
• Forecasting and Hindcasting.

The result of the reanalysis process is that the physical state of the entire global atmosphere is estimated hour-by-hour extending back many years. And the record is added to every day as a by-product (a reanalysis) of the calculations used for weather forecasts.

• Please take a moment to consider the mind-bending scale of this undertaking.

The ‘Pulse’ Web Site that generated the images at the head of the article is an interface to one small part of a reanalysed data set established by the European Centre For Medium Range Weather Forecasting called ERA5;

ERA5 provides hourly estimates of a large number of atmospheric, land and oceanic climate variables. The data cover the Earth on a 31 km grid and resolve the atmosphere using 137 levels from the surface up to a height of 80km. ERA5 includes information about uncertainties for all variables at reduced spatial and temporal resolutions.

The full list of ‘products’ that can be derived from this data set goes way beyond the simple quantities and runs to 263 ‘main’ quantities including wind speed and direction at different heights, and rain, snowfall and sunshine.

The ERA5 dataset extends back to 1940, so that if you wanted (for some reason) to know what the weather was like (windy, rainy? sunny?) in (say) Wolverhampton on (say) 18th September 1957 at 11:00 a.m then the answer would lie in one or more of its ‘products’.

More practically, reanalysis technology is behind the European Sunshine database which will give an hour-by-hour estimate for how sunny it was at on any location on Earth (!) between 2005 and 2020. This reanalysis ‘product’ allows one to calculate the expected yield from solar panels placed in any orientation anywhere on Earth.

Climate Datasets are not Reanalysis Products

The hour-by-hour estimates for land-surface air temperature and sea-surface air temperature can be averaged to produce daily, weekly, monthly, or annual estimates. And these data can be shown on maps to show the ERA5 estimate for how different parts of the Earth have warmed in (say) 2023.

The figure below shows the ERA5 estimate for the temperature anomaly across the globe in 2023. To create the image, the ERA5 average air temperatures above the land and sea surfaces of the Earth are calculated for (a) 2023 and (b) the period between 1991 and 2020. The plot shows the difference between these two quantities at each location, with red and orange colours showing areas which have warmed, and blue colours showing areas which have cooled.

Click on image for a larger version. Image from the Copernicus ‘pulse’ web site showing estimates for the anomaly in the global air-temperature (just above the land or sea surface) i.e. the difference in the global air-temperature averaged using all the data from 2023 and the average result for the period 1991-2020.

Images such as the one above are commonly seen on news reports and social media – often because (like the images at the head of the article) they are updated daily and so constitute ‘news’. However, it’s important to distinguish between these images and other apparently similar images produced from climate records.

For example, the image below is apparently similar to the one above, showing the air temperature anomaly above the land and sea, but it has been derived in very different way. Over land, the data is derived solely from meteorological stations and over the sea the data is derived from marine buoys and ships.

The meteorological data are recorded at a variety of rates: some is recorded every 10 minutes, some hourly and some just twice a day. From this data, daily averages are calculated, and these are then further averaged over (typically) a whole month. Because the meteorological stations are not distributed uniformly around the globe, the data are pooled to give a fair estimate for the temperature anomaly on a uniform grid. Note that in the figure below there is much less fine detail visible than in the ERA5 estimate. Note also that (irritatingly) the 2023 data in the figure below is compared with the average temperature during the period 1951-1980 unlike the ERA 5 estimates which are compared with the period 1991-2020 .

Click on image for a larger version. Image from the Berkeley Earth web site showing estimates for the anomaly in the global air-temperature (just above the land or sea surface) . In this case the data show the difference in the global air-temperature averaged using all the data from 2023 and the average result for the period 1951-1980.

Climate Datasets versus Reanalysis

So there is more than one way to estimate the warming of the Earth’s surface.

The ‘traditional’ way to do this is by analysing meteorological station data, taking monthly averages, and then eventually comparing annual averages with earlier data. This is how Guy Callendar first detected the warming of the Earth in 1937 – doing all the analyses by hand! Nowadays, this is a much larger undertaking since there are roughly 30,000 meteorological stations. These datasets are typically updated about a week after the end of each month. The strength and value of this approach is that there is direct traceability between the results and the source data.

Using reanalysis techniques, the underlying dataset is updated daily and runs about three days behind the current date. The reanalysis dataset contains hundreds more variables – not just pressure temperature and humidity – and is estimated with a much finer spatial and temporal resolution. However the traceability from the source data to the data product is more complex.

Using the ‘dashboard of dashboards‘, you can link to UK Meteorological Office Dashboard and see how ERA5 compares with other reanalysis endeavours and traditional estimates of global warming. The ‘discover more’ button will give you lots of information about the underlying datasets, but the basic graph shows that all the datasets – no matter what method is used – agree well.

Click on image for a larger version. Image from the UK Met Office web site showing estimates for the anomaly (in °C) in the global air-temperature (just above the land or sea surface). Each line represents and independent analysis of the data including ERA5 and Berkeley Earth. In this case the data show the difference in the global air-temperature compared with the average result for the period 1850-1900.

The agreement between the different estimates of global temperature is both reassuring and disturbing: it’s good to know that the different analyses agree – but the message they are telling is still pretty terrifying.

Big Storm

Friends, today I offer you a song about Climate Change: Big Storm. (You Tube Link). If songs aren’t your thing, don’t worry, normal service will be resumed presently.

I spend a lot of my time writing and singing and recording songs. It’s a time-consuming business, but it is nothing compared to the hassle of making a video. This video passed the low bar I set for “good enough”, but I am aware that the lip-synching is poor, and that I occasionally become slightly transparent! There is also much more of my own face than I feel comfortable with. I can imagine a much better video – but I don’t have the technical ability to make it!

Nonetheless, I like the song. I hope you enjoy it too.

Big Storm Lyrics

There’s a big storm coming, I can feel it in the air.
If you care to look around, you’ll see the signs are everywhere.
There’s a big storm coming, it’s getting closer every day.
Stay with your family, you could all… be blown away.

Climate change is with us, Climate Chaos everywhere.
Climate Change Deniers on TV swear round is square.
Climate change is with us, feels like there’s no relief.
We’ve made a deal with the devil, and he’s turning up the heat.

There’s a big flood coming, the water’s rising every day.
Slow and relentless, that’s water’s way.
There’s a big flood coming, but you’re not ready yet.
No-one thinks the flood will really come… until their feet get wet.

The climate we grew up in, is gone, never to return.
The meadows we once wandered in, will turn to dust and burn.
The Good Earth once provided us with everything we need.
But now we’ve sacrificed its future, on the altar of our greed.

There’s long hot summer brewing, the grass has turned to straw.
Farmers are complaining, nothing’s growing anymore.
There’s long hot summer brewing, and we all know why.
No-one thinks the drought will really come… until their taps run dry.

Climate change is with us, Climate Chaos everywhere.
Climate Change Deniers on TV swear a circle is a square.
Climate change is with us, and there’s no relief.
We’ve made a deal with the devil, and he’s turning up the heat.

 

Kevin ‘Heat Pump’ McCloud

Friends, from time to time we are all in need of a little positivity – and so today I offer you the most positive form of video known to humanity: the advertorial. More specifically, three heat pump advertorials featuring Kevin McCloud.

When I feel too emotionally fraught for mainstream TV, I occasionally switch to a shopping channel. There, people with real problems – such as the inability to clean grime from their kitchen tiles – have their lives transformed by the utility of a 3-in-1 thingy. Not only does the 3-in-1 thingy solve their grime problem, but it also solves other problems they perhaps didn’t know they had. And the version on sale today comes with a four metre extension! And is available in three easy payments.

Of course this portrayal of transactional happiness is shallow and associated with our culture of perpetual consumption. But occasionally, the presentations show a sufficient facsimile of happiness to lift my spirits momentarily.

And so we come to Kevin McCloud. 

The three videos below feature Kevin McCloud describing three installations of Vaillant Arotherm plus heat pumps. They are not documentaries, but more like mini-episodes of Grand Designs – skipping all the stuff about running out of money and living in a caravan.

I present them to you because I find them calming to watch – they show happy people with heat pumps, and that’s something we all need to see more of!